 The movie 21 introduced many to the concept of variable change. But what is variable change? Stay tuned for a lively discussion!
The movie 21 introduced many to the concept of variable change. But what is variable change? Stay tuned for a lively discussion!
During the movie 21 (read my 21 movie review here), we are introduced to a seemingly simple example of probability often referred to by three different names: Variable change, the Monty Hall Problem, and/or conditional probability. The scenario is this:
A game show host tells a contestant to choose between three doors. Two doors have a goat behind them…and the other has a brand new car. He tells the contestant to choose a door. The contestant chooses door #1. Then, the host, knowing what is behind each door, reveals what is behind door #3-a goat. He then asks the contestant if he would like to change his choice or stick with door #1.
What would you do?
As mentioned, this mathematical scenario is known as The Monty Hall Problem and is an example of the principal of variable change and conditional probability.
My initial thought would be to stick with door #1 as it was the original hunch and the probability is 50/50.
But this is the wrong answer as the probability is not 50/50, which surprised me and has confounded many on the Internet. As you’ll hear in one of the variable change explained videos below, the narrator states: “It’s an example of math completely contradicting my guy instinct!”
And on the message boards for the movie 21, there are more than 10 pages of discussion regarding this very point. Also, below you’ll find nearly 100 comments with this theory of variable change heatedly debated (make a comment below yourself if so inclined).
Who says that everyone these days is intellectually apathetic?
The right answer? You should always change to door #2 because the probability that the car is behind door #2 is greater: 66.6% to 33.3%.
Why is this?
Well, we all know at the beginning that the probability that the car is behind the door that we choose is 33.3% or 1/3.
But then, then the host reveals that there is a goat behind door #3 and we have just two choices, which most of us assume have an equal chance of having a car behind them. But they do not and the graphic below illustrates why.
When you begin, here is what your odds looks like:
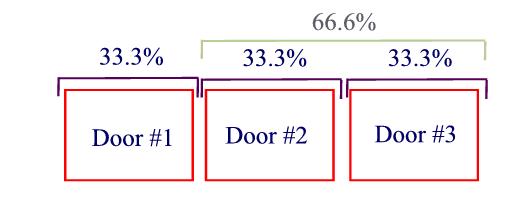
However, after door # 3 is eliminated, you are left with doors one and two. You can see in the diagram below why door #2 has a 66.6% chance and door #1 remains at 33.3%:
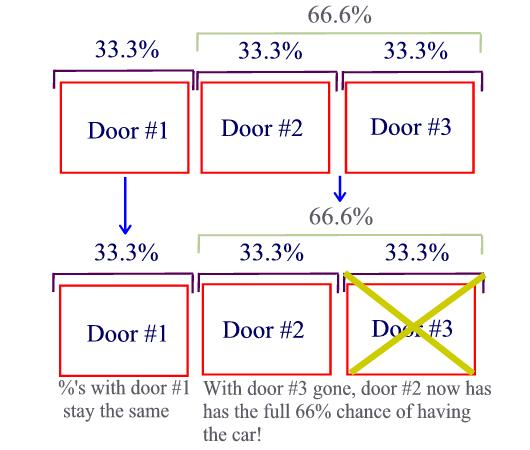
This scenario illustrates the principal of variable change.
Of course, you still might get it wrong, but at least your odds are better.
I’m not a statistician, so if you agree or disagree, feel free to comment and you’ll definitely want to read the comments below, where people engage in lively debate about the nuances of variable change.
Links Related to This Scenario:
Monty Hall Problem: Read a history of the problem and solution on Wikipedia.
Wednesday Math, Vol. 23: The Monty Hall Problem: Matty Boy also discusses the issue on his blog after seeing the movie 21.
The Monty Hall Problem: Discussions from a Mathematics Professor.
Let’s Make a Deal: Here, you can play a simulation of the game.
Videos: What is Variable Change & the Monty Hall Problem?
Explained: The Monty Hall Problem & Variable Change
In this video, we learn the counter-intuitive answer to The Monty Hall Problem and the concept of variable change.
Monty Hall Problem by Lisa Goldberg
The variable change dilemma as expressed by Lisa Goldberg, an adjunct professor in the Department of Statistics at University of California, Berkeley.
The Monty Hall Problem Explained
What is variable change? This is another great video that explains and illustrates the variable change theory.
What do you think of this Monty Hall problem and the theory of variable change? Would you change your initial pick? Chime in with thoughts in the comments section below.
Richard Cummings
Get your copy of his latest book entitled Obvious Conclusions, stories of a Midwestern emigrant influenced and corrupted by many years living in San Francisco and abroad. It just received its first outstanding review "...reminiscent of David Sedaris or Augusten Burroughs" on Amazon UK.
Latest posts by Richard Cummings (see all)
- The Google Pixel Fold: Why It’s the Star of Google I/O 2023 - May 9, 2023
- Book Review:Malibu Rising by Taylor Jenkins Reid - March 6, 2022
- Beautiful World, Where Are You: A Book Review by Richard Cummings - February 18, 2022


Comments 102
The explanation is wrong in the sense that you have added up the probabilities of having the car behind door 2 or 3. The very fact that door 3 does not have a car behind it does not allow you to simply add the probability of success to door 2.
Let me ask a question: If I chose door 2 initially and later it was reveiled that door 3 had a goat, then by your logic finally door 1 should be ending up with 67% probability of having a car. Now it seems that my initial choice of door is affecting the odds of having the car behind a door.
Thats why probability is finally 50%. Whats shown in movie is wrong.
Wrong.
First, from the probability standpoint, the probability of a car behind door one is ~33%. That also means that the probability of a car NOT being behind door one is ~66% (one minus the probability of the car being behind door one, i.e. 1-~33%=~66%). That is, the first choice of door one is ~66% incorrect. The probabilities are not added together for correctness; they are the probability of door one incorrectness.
The idea is completely misunderstood. It is not the probability that changed. The probabilities remain the SAME. The probability of being correct and the probability of being incorrect. These are not dependent probabilities. The NUMBER OF VARIABLES CHANGED. The probability of being incorrect on the initial selection of door one is still ~66%.
Bayes’ theorem does not apply.
Nope. It’s sleight of hand. The same probability of Door 2 being wrong is the same 66.6%. Even after eliminating door 3.
Only one variable changes. The number of doors available, the 33,3 % chance indeed adds into the other 2 doors equally. the possibility of there being a car (presumably if there is indeed a car behind a door) remains 100%. Going down to only 2 options.
I just read the theoretical proof which I should have looked for. The result is indeed correct. But again the method for proof in this blog is not at all trustworthy. for proof refer http://en.wikipedia.org/wiki/Monty_Hall_problem#Bayesian_analysis
To analyze this problem with much more accuracy
Lets extend this problem to 10 doors where car is behind one of them and remaining are empty.
You are asked to pick a door and suppose you pick door number one(1) or which ever you want.
Now see carefully,
There is
10% chance that car is behind the door you picked and
90% chance that car is behind one of the remaning doors you did not pick
Now remember that host knows which door has car behind it and he opens 8 doors from those which didn’t have car behind them and the door with car is kept close no matter that door is door number 2 or 3 or 4 or 5 or 6……..
Now host asks you if you want to change your option,
if you stick on your option, then there is 10% chance of winning
if you change your option, then according to statement 1,there is 90% chance of your win.
If you are clear then its ok other wise see this table
here 1 represents car, zero represents empty door
*Note: These are all 10 possible configurations for car placement
Each of these configuarations is equally probable
door1 door 2 door3 door4 door5 door6 door7 door8 door9 door10
1 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 1
suppose u pick door 1, and stick to your choice then only for first configuration you will win and for remaining 9 configurations host will open 8 doors with no car behind them you will lose. your winnig chance is 10%
If you choose to change your options then you will win for 9 configuration and loose for only one.your winnig chance is 90%
This is an awesome explanation of the idea. With the implication that the host knows the door the car is behind. He then picks all of the other doors besides the one with the car and the one that you picked. Thus increasing the chance that you originally picked the wrong one being 1 out of 10. The host would not just show the door you chose because, where is the fun in that. So the host reduces the equation down to the last two doors. You think it is 50/50 when actually the host has narrowed the margin down to the 90/10. The only way you are screwed is you picked the first one off the bat. Which would be one in ten. The problem is not mathematical, the problem is the human/entertainment part of the equation. The host knowing where the car is. If the host was un aware of where the car was and chose randomly, now we just have the math. At anytime the host may revile the car and not just choose doors it was not behind. Human psych vs math. Know the rules you are playing by.
I think the simplest way to understand this is the following:
You have a 66.67% of NOT picking the door with the car at the beginning.
If the door that you pick at the start does not contain the car then the car MUST be behind the door that the host does not open.
Therefore if you always trade doors then your give yourself a 66.67% chance of winning the car.
It is misleading. It is accurate ONLY IF, but only if you assume Monty HAS to open one door. The problem with the 21 movie is that you do not know if Monty has to do so. If he doesn’t, and knows that you picked the car the equations are inaccurate because the above equations presume he has to pick one door to open. If you don’t know if he has to open one door, the probabilities under this scenario reset to 50/50.
The way I see it, there are 3 rules the game show host must follow for the 2/3 chance to be accurate and none of them are explicit from the way the problem is stated in the movie.
1) Whether the game show host opens a door is not dependant on the choice of the first door (this is basically what svenn said except it would still work if the game show host flipped a coin to see whether he opened the door, but not if he opened the door only if you picked the door with the car)
2) The game show host will not open the door you chose
3) The game show host will not open the door with the car behind it
These may seem obvious to some people based on the game show premise and the fact that the host knows where the car is, but if you don’t know the system that’s being followed then you are back to 50%.
I used to work at shodor, they’ve got a lot of different math “activities” that illustrate things like the Monty Hall Problem. You should note that the higher the number of tries the closer you get to the 67% win percentage.
http://www.shodor.org/interactivate/activities/AdvancedMontyHall/
There are many ways to explain why your probability of winning the car is in fact 66.6%. I find this easies to understand:
Here is the key: Given the rules, if you always switch your pick, your first choice will always determine if you win or not.
(1) If your 1st choice is a goat, you will always win the car. This is because the host will reveal the other goat so when you change, it will ALWAYS be to the car.
(2) If your 1st choice is the car, you will always lose. This is because the host will reveal a goat so when you change, it will ALWAYS be a goat.
Therefore: Since your odds of initially picking a goat are 66.6%, your odds of winning the car accounting for variable chnage is the same – 66%.
Not the simplest concept to understand but, it is obviously true.
most of the comments on here are correct. I did a search on it, primarily because in watching the way it was portrayed in the movie, that it couldnt be correct.
The only way it can be correct is to assume that the host will point out a goat to begin with, which wasn’t stated in the film. Once you can safely assume that, you can increase your odds by switching.
Here’s an explanation in a different way that I wrote up to try and explain this problem to people from a different angle so they could grasp it better. The problem is human understanding in time in terms of seconds rather than metres, so just put that out of your mind for a second and bear with me:
======================================
Answer to the question about variable change introduced by the movie “21”:
———-
The professor tells the main character that he is on a game-show and the game-show host tells you he has 3 doors: Door 1, Door 2 and Door 3. Behind one of the doors is a sportscar. Behind the other two doors there are goats and he asks you to pick a door at random. The person chooses Door 1. The game-show host then opens Door 3 and reveals that is has a goat in it. He then asks if they want to keep their initial answer of Door 1, or switch their choice to Door 2?
The person explains that it would double your chances of winning if you switched the cases. Why?
———-
Wow… so many confused people… I love it! Let me explain it a different way that will clarify any doubt. The REASON that you are all confused is because of the temporal variables that are irrelevant here.
Consider an equivalent scenario mathematically, but COMPLETELY different, temporarlly and the answer will become blazingly obvious and you will slap yourself in the forehead and say D’oh! Of course!
Imagine if the host did NOT reveal the goat FIRST, but AFTER you decide whether to switch or not. It doesn’t matter WHEN the host reveals the goat, the point is that he’s going to reveal a goat, and regardless of that, you get to pick which “set” of doors to go with.
Consider what’s really happening here. You are dividing the doors {1,2,3} into two sets. The first set is {1}, and the second set is {2,3}. Now, given this division, which set of doors would you choose?
Well obviously you’d choose set {2,3} because it is more likely that the car is in one of those two than if it is in door {1}. The host could just have easily said:
Host: Pick a door
Contestant: I pick door 1
Host: Ok, now given that you have picked door 1, which do you think contains the goat? Door 1? Or one of the other doors?
Contestant: Well it’s probably in one of the other doors
Host: Ok, I will let you pick EITHER of the other two doors and if it’s in EITHER one of them, you win (because I’m going to show you LATER which one has the goat and you can have the other door which has the car no matter whether the goat is in 2 or 3)
Contestant: RIGHT ON! I’m going with the set of doors {2,3}, thanks for the extra 33% chance of winning host!
Yes, I know this problem was tricky… it was set up with all those temporal variables to purposely try and confuse a human mind which has an erroneous concept of time to begin with.
Were time measured in metres, nobody would find this confusing at all.
The solution that is spoken of in the movie is wrong to anyone versed in statistical probability. There is something referred to as the law of replacement. Anecdotally, the movie is correct, scientifically, the solution is not sound due to the law of replacement regarding probability. If you remove one of the probabilities of an equation, you automatically reconfigure the statistical odds as you did not replace the probability. By the sheer fact that there are only two choices left, and not three, by definition, the odds are now 50%.
I CONCUR WITH IMANI…
REGARDLESS OF WHAT THE PROBABILITY STATS ARE AT THE BEGINNING DOESNT MATTER. AFTER HE SHOWS THE GOAT BEHIND WHATEVER DOOR. THAT DOOR IS TAKEN OUT OF THE EQAUTION. SURELY YOU DONT COUNT THIS IN YOU CHOICE ANYMORE. LET ME SEE…HMMMM…DOOR 1 HAS A GOAT SO I SHOULD TAKE THAT INTO CONSIDERATION FOR MY OTHER TWO CHOICES. NO!!! NOW THE PROBLEM BECOMES CLEARY A CHOICE BETWEEN TWO DOORS. WHO CARES ABOUT DOOR 1. WHAT IF YOU WALKED IN AFTER THE TEACHER SHOWED THE DOOR. IS IT STILL 66.7%. NONSENSE. YOU WALK IN TO THAT PROLEM, YOU SEE…TWO CLOSED DOORS, ITS A 50/50 CHANCE TO GUESS THE CAR. YOU DONT LOOK AT AN OPEN DOOR AND SAY…WELL IF I THROW THAT ONE IN. WHEN THE TEACHER SHOWS THE DOOR IT MAKES IT A TOTALLY DIFFERRENT PROBLEM. 50/50. AM I MAKING SENSE…DESTROY ME IF YOU WILL. I WANT TO THINK LIKE THE REST OF YOU…ESPECIALLY IF IM WRONG. BUT I DONT SEE IT….AAAAHHHH I ONLY SEE 50/50 HELP
Dr. Jerky – you are not taking something into account. If you walked in after he had opened one of the doors, the probabilities are still going to be 33/66, but you just won’t know this. Being oblivious of the actual probabilities does not change the probabilities. There is a 66 percent change of the car being behind door #2 because there was a 66% chance of it being behind the set {2,3} to begin with. Stop thinking about it in terms of two independent probability problems.
The problems are NOT INDEPENDENT.
For instance, if they were independent, then the host could open the door with the car by accident, but he can’t. Why not? Because the two problems are really one problem with a confusing sequence of discoveries.
Think of it like this. The probability that the car is behind door #1 is 33% at the beginning, right? RIGHT! How can that probability suddenly change, just magically, mysteriously just because you peeked behind one of the doors? It can’t. The probability that the car is behind door #1 is ALWAYS 33% throughout the whole sequence of operations. It doesn’t just suddenly change to 50%, how would that happen? Your probability background should tell you at least that much. It would be like being clairvoyant somehow, and statistics does not involve clairvoyance. That’s actually your whole argument… that the probability of door #2 can’t suddenly change to 66%, right? So why would you say that door #1 can suddenly change from 33% to 50%??
Now… think about what is actually happening… the probability that the car is behind door #2 is only changing because door #3 has been taken out of the equation. That 33% chance that the car was behind door#3 has to go somewhere because you can’t have 33/33 – it doesn’t add up to 100.
Think of it this way, as some other poster mentioned:
Imagine 1000 doors.
Pick one of those doors. Door #1.
Now we know that there are goats behind at least 998 of the other 999 doors. So open all those goats.
You’re left with Door #1 and Door #237. Do you think you now have a 50% chance of having picked the EXACT right door right off the bat? I doubt it. You probably picked wrong, which means the car is probably behind door #237 and the host is basically giving you that for free because he got rid of all the goats for you.
In a nutshell:
Your probability of having picked the right door to begin with does not suddenly jump to 50% just because somebody “in the know” removes all the goats from the equation
The Movie is correct and is based on a true theory. Look at it the easiest way possible.
The doors are as follows C=Car G=Goat
C G G – Lose
You pick Door 1 and switch to door 2 after the Host Takes away 1 goat.
G C G – Win
You pick Door 1 and switch to door 3 after the Host Takes away 1 goat.
G G C – Win
You pick Door 1 and switch to door 2 after the Host Takes away 1 goat.
There you have it. if you switch you have a 2 in 3 (66%) chance of winning.
IF YOU DO NOT SWITCH THIS IS WHAT HAPPENS
C G G – Win
You pick door 1 and do not switch to door 2 after the host takes away door 3
G C G – Lose
You pick door 1 and do not switch to door 2 after the host takes away door 3
G G C – Lose
You pick door 1 and do not switch to door 3 when the host takes away door 2.
You only have a 1 in 3 chance (33%) if you do not switch.
Here it is Plain and Simple for those who still think you have a 50% chance no matter what. Enjoy
No Its CG1G2, G1CG2, G2CG1, CG2G1 Those are all the instances a goat is behind door three. It leaves you with an equal chance of getting a C or either G1 or G2. 50/50. You are treating both goats as one. Let’s say it was a goat or a pig. Both goat and pig are undesirable (like both goats would be). Its is CGP, CPG, PCG. GCP…this is the way the host could open #3 and find an undesirable choice (either G or P). That leaves you with CP, CG, or GC, PC. equal chance. 50/50.
Correction
in the 1st set of 3 options i had the #s wrong. Heres how it should be.
C G G – Lose
You pick Door 1 and switch to door 2 after the Host Takes away 1 goat.
G C G – Win
You pick Door 1 and switch to door 2 after the Host Takes away 1 goat.
G G C – Win
You pick Door 1 and switch to door 3 after the Host Takes away 1 goat.
My Bad.
66% it is!!!
Wrong. Because you don’t identify the two different goat, you miss options.
C G1 G2 – Lose
You pick Door 1 and switch to door 2 after the Host Takes away 1 goat (G1).
C G1 G2 – Lose
You pick Door 1 and switch to door 3 after the Host Takes away 1 goat (G2).
G1 C G2 – Win
You pick Door 1 and switch to door 2 after the Host Takes away 1 goat (G2).
G1 G2 C – Win
You pick Door 1 and switch to door 3 after the Host Takes away 1 goat (G2).
The chance is always 50/50 by the rules. The game only starts after one goat is taken away by the host. Then your choice is between the goat and a car. You don’t increase or decrease your probability here.
my self and my colleagues had a discussion about this subject, with different opinions, obviously. we know that when you create a test medium which happens to confirm your theory, then you have the right to think that you are right. my self, being a programmer, i wrote a small script to test the cases where a player would a) change the door, b) stick with the first choice and c) choose random every time.
result tests show that the theory is right: 66% chance of choose right if change the door, 50% if you choose random every time, 33% if you stick to the first choice; with some deviations of course, but it is pretty relevant.
should my programming be bad, hopefully someone will correct me, though i do not think it is the case.
if anyone likes to test that, just copy the content of the script from http://rafb.net/p/chIo2328.html, put in a text file with the extension *.py and just run it. obviously you will have to have the python program installed on your machine (available for free at http://www.python.org/download/)
Um I understand the groupings and the percentages and all but if you know the game show host will always reveal a goat out of the three doors then your chances at picking the correct door is still 50/50! If you actually do account for a variable of change and a variable of occurance (that being the host always reveals a goat) you know you are still stuck with a 50/50 chance of picking the car!
Might I add, if the game show host did not I repeat, DID NOT know what he would reveal as he opened one of the doors and he revealed a goat then and only then does their arise an increased propability that the car is in the door you did not choose.
for instance: some say
door 1 = 33%
door 2 & 3 = 66%
and host reveals 3 as a goat you should theoretically pick 2 as it falls in the 66% grouping increases your chances but I say that line of thinking is flawed! For if you know the game show host will reveal one of the other doors within the 66% group (the doors you did not choose) as a door it re-categorizes the percentages and gives them an equal value of 50% thus making ur chances on choosing the car at 50/50!
The whole theory rests on the possibility of what the host will reveal. If it is at all possible the host would reveal the car then this variable of change theory would apply and I would thus switch my original choice!
My brain hurts! ;P
You can use the same argument to show that door 1 to prove that door 1 has a 66% chance of holding the car. Obviously, there is something wrong with the argument since door 1 and door 2 both can’t have a 66%% probability of being correct.
For example:
When I chose door 1, I was actually choosing the set {1, 3} which has a 66% chance of having the car in it. Since door 3 had a goat, door 1 now has a 66% chance of having the car and door 2 has only a 33% change of having the car.
Clearly this line of reasoning must be can not be correct because it can be used to “prove” that both door 1 and 2 are the best choice.
Once Monty reveals that door 3 has a goat, it is removed from the problem and the contestant is faced with an entirely new choice: two doors each with a 50% chance of holding the car. The key to understanding this is that there the second choice is not a continuation of the intial problem, it is an entirely new problem.
> When I chose door 1, I was actually choosing the set {1, 3} which has a 66% chance of having the car in it. Since door 3 had a goat, door 1 now has a 66% chance of having the car and door 2 has only a 33% change of having the car.
WRONG. When you chose door 1, you were splitting the set into {1} and {2, 3}, therefore the set {2, 3} has a 66% probability of being correct, and the set {1} only has a 33% probability of being correct.
> Clearly this line of reasoning must be can not be correct because it can be used to “prove” that both door 1 and 2 are the best choice.
The set of doors {1, 2} DOES have a 66% chance of being correct. Had the division been made in this fashion (ie: by the contestant choosing door 3 initially), then YES absolutely he should switch to the set {1, 2}, rather than sticking with his original choice of {3}.
I don’t understand how people don’t understand. Forget the math you think you know, or learned once long ago in school. This is too simple to theorize.
Try using some common sense.
If there are three doors and behind one contains a car, would you like to pick one door OR do you think your odds of winning might be better if you chose two doors?
If you think your odds are better by choosing one door, then I’d like to play this game with you for real. Any takers?
Owned.
Jack, nice try but you got it wrong.
You aren’t given that choice at the beginning. You make your first choice when it is a one in three chance. You then make another choice when it is a one in two chance.
Your argument would ONLY be right if you were offered door one or doors two and three BEFORE any have been opened. Before you make your choice there is a two-thirds probability that doors two and three have the prize but once you have removed one of those then it is 50/50 between the remaining choices.
I don’t understand how you can’t grasp this most basic concept?
I can appreciate why people think the answer is the way it is but it’s an optical illusion for the brain.
Martin, actually Jack is right. You ARE given that choice in the beginning. When the host removes the goat from the equation, he essentially turns back time and makes the probability of your next choice change – hence variable change. The ONLY way what you are saying would be true is if the host picked a random door to remove, which means he might remove the car. Since this is not an option, the host’s choice is NOT random, and hence changes the variables in the equation.
The easiest way to think of it is imagine 1000 doors. You pick one of the doors, the host removes 998 other doors with goats. Do you think you now have a 50/50 chance that you picked the car in the first place when there were 1000 other doors? I think not.
Svenn and patti got it correct from a math point of view. the problem was not stated correctly in the movie. Those that have taken probability knows that you must examine if the outcome of one trial affects the outcome of the next. For instance when you roll a dice the chance of rolling a 5 is always 1/6. Each role is independent of the other. So in this case it seems it would be 50% because you are picking 1 out of 2 doors.
I think this is what Imani and Dr. Jekyl are thinking. It is what I thought after watching the movie. But as stated by Svenn and patti, the rules of the game means that the previous outcome has an effect on the next outcome because the game show host knows where the car and will not be picking at random, therefore the trials are not independent of one another.
finally there is this site
http://www.shodor.org/interactivate/activities/SimpleMontyHall/?version=1.6.0_05&browser=MSIE&vendor=Sun_Microsystems_Inc.
play and you will see the probability of 66% when you switch doors. Notice how the game never picks your door, it always picks one of the other 2 doors which has a goat. That is the key to understanding the problem
Drew, I am an enthusiastic but rather mediocre first year maths student who very much appreciated your explanation, which makes perfect sense. I think if you combine the idea of sets with an increase in the number of goats (doors) involved, it does become quite intuitive. Thanks a lot. Also gunoieru simulation always helps too!
Ok People, I graduated from high shcool, started college and realized building houses was my gift. Needless to say I work with quit a few non graduating high school students. So sometimes I need to explaing myself clear in all languages, even when I only understand English so so. Lets go guys and girls stay with me.
When the game show host first gave us three doors to choose from I feel not one of us had a problem feeling we had a 33.3% chance of picking the right door. why did you and I say 33.3% chance of winning because 3doors X 33.3% = 100% right.
Now when door 3 is opened and is a goat that 33.3% needs to be eliminated from the starting point and needs to be divided equally in half which is 16.65% and added to door one and two evenly, which now brings doors one and two up to 50% each. Cut and dry. If I picked door one and my girlfriend picked door two and we both switched to the other door that would mean I would have a 66.6% chance and she would have a 66.6% chance of winning. 66.6% + 66.6% adds up to 133.2% now can we all see that this is not possible. Can we see that 133.2% would sound like a politician speaking. I hope you all can see this now in what ever language you read or what ever politician you are hearing. 133.2% is not what it can be. It can only be 100%. If I change my door and get 66.6% you can be rest a sure my girl friend will want her 66.6% as well. This is the problem we all want more than 100% and no one can give us more than 100%. Therefore door two can not get the 33.3% added to it and door one get nothing right?
Hi there Rob, I see what you are saying, but you’re forgetting one thing. If your girlfriend had picked door #2, it probably would’ve been your door #1 that would’ve been opened with a goat, so you can’t think about it that way. It goes ONE person at a time, not two. The reason is because the door that the host opens depends upon where the car is. The host is tricking you. He’s gonna change his door selection so that it will always be 66.6% chance of it being the door you didn’t pick. That’s the catch.
Let me try to explain a different way.
Say you pick door #1 initially. We all agree that you have a 33% chance of winning the car. Then you ask the host to go behind the stage and find a goat and tell you which door has that goat. Do you think the act of the host looking behind the stage suddenly changes the 33% probability that you picked the car? Of course not, you said so yourself in your message. You have 1/3 chance that you picked the car, ALWAYS, no matter what happens. You can NEVER change the past and that 33% is FIXED IN STONE. So stop thinking of it like that. The 33% does not change to 66%, it does not change to 50%. It STAYS 33% and has to.
What does change is that the host was kind enough to let you pick the TWO doors (door #2 AND door #3). So when he asks if you want to change, he’s not asking, do you want to switch from door #1 to door #2. He is ACTUALLY asking, do you want to change your selection from door #1 to BOTH door #2 AND door #3. And of course you’d say yes, because picking two doors is always better than picking one.
It becomes super easy to visualize when you think about 1000 doors. You pick door #1, and then the host goes and removes goats from 998 of the other doors, leaving only door #1 and door #237. Knowing that there’s a car behind one of them, do you want to change your selection to door #237? Or do you want to stick with your original choice of door #1 and hope to heck that somehow the probability jumped from 1/1000 to 50% magically just cause somebody went behind the stage for a minute???
When in doubt, use brute force.
I created a table where I mapped out every possible permutation of the problem. There are only 24 possible outcomes, and in 12 of them staying the correct choice, and in 12 of them switching is the correct choice. 50/50.
http://www.andrewcmurphy.com/monty_hall.html
First of all, I agree with the switch, but only if the host opening one door is constant. If the host has a choice of whether to open a door or not then you don’t switch. I’ll be the host and we’ll play 1000 times. I’ll open 1 door after you choose and give you a choice to switch 100 times out of the 1000. You switch every time you have a choice. You won’t win once out of the 100 becuase I can’t afford to give away a car. You must know whether the host intended to open a door no matter what door you picked in order to gain an advantage by switching.
If the host opening a door is a constant, if you switch every time then you win if you were wrong on your first choice and lose if you were right. 33 percent you were right and 67 you were wrong, so 67 percent you win and 33 you lose.
You would still feel the fool if on game night you swapped doors but the car was behind door #1. You could discuss probability with your mates at the bar and explain to them that if you repeated this process 2 more times you would have won the car twice!
Andrew, you have made an error in your analysis. You are counting the scenario where you picked the correct door initially twice. If you look at the row of numbers in your table denoted by “Your initial pick is door number:”, you will see that you are giving a 50/50 probability for having selected the correct door initially, which is wrong. It is a 1/3 probability for having selected the correct door initially.
You are essentially asking the question “Given that I have a 50/50 chance of having selected the correct door right off the bat, what is the likelihood that switching doors will make me a winner?”.
To the player, it is unknown whether the host knows whether which door has the car as not stated in the problem statement.. In this scenario, the probability that the host knows which door has the car, to the player is 1/2. Now if the host does not know which door has the car behind, the probabilities of the player’s winning or losing by keeping the 1st door is the same i.e. 1/2 when the host reveals that the 3rd door has the ghost. In case the host knows which door has the car, behind, the player indeed has a winning probability of 2/3 on switching according to simple Bayesian analysis.. Hence the cumulative probability of winnin will be..
Probability of host knowing the door having car X 2/3 + probability of the host not knowing of it X 1/2 = 1/2*2/3 + 1/2*1/2 = 1/3 + 1/4 = 7/12
Probabilty of losing hence would be 1-7/12 = 5/12 which can also be proved in the manner stated above.
the easy solution is as following :
the host reveals a goat and you switch, what is the probability to win ?
Probability to win =
(1) you picked the car : switch = 100% lost ==> 1/3 x 0
(2) you picked goat number 1 : switch = 50% win and 50% lost ==> 1/3 x 50%
(3) you picked goat number 2 : switch = 50% win an 50% lost ==> 1/3 x 50%
(1) or (2) or (3) = (1) + (2) + (3) : OR = + while AND = x
1/3×0 + 1/3x 50% + 1/3×50% = 2/3
correct solution =
the easy solution is as following :
the host reveals a goat and you switch, what is the probability to win ?
Probability to win =
(1) you picked the car : he shows you goat number 1, your switch = A LOST (because you switched to the other goat)
(2) you picked goat number 1 : he shows you goat number 2, your switch gives you the car = 100% WINNING
(3) you picked goat number 2 : he shows you goat number 1, your switch gives you the car = 100% WINNING
So you do not know what is behind your chosen door :
meaning :
1/3 x 0% winning + 1/3 x 100% winning + 1/3 x 100% winning = 2/3 x 100% winning
==> P(winning when switching) = 2/3
Variable Change – Big words for conditional Probability Calc
When you pick 1 door, the Probabilities are :
P(car)=1/3
P(Goat 1)=1/3
P(Goat 2)=1/3
Now, Monty opens a door with a goat,
Switching your choice means “What is the probability that the other door is the car ?”
OR : you originally took the car AND switch
P(successful switch under this knowledge)=0,
P(successful switch/you took the car) = 1/3 x 0
OR : you originally took Goat 1 AND switch
P(successful switch under this knowledge)=1
P(successful switch/you took Goat 1)=1/3×1
OR : you originally took Goat 2 and switch
P(successful switch under this knowledge)=1
P(succcessful switch/you took Goat 1)=1
OR = +
so P(successful switch/you took random door) = 1/3×0 + 1/3×1 + 1/3×1
= 2/3
Think of it this way if you switch…
Scenario 1:
You choose the car. (There is a 33% chance of this happening.) The host reveals one of the remaining goats. You switch your guess and pick the other remaining goat. You loose.
Scenario 2 and 3:
You choose either of the goats. (Both goats include 2 of the three options so there is a 66% chance of picking a goat.) The host must reveal the remaining goat. You switch and pick the car. You win.
Think of it this way if you don’t switch…
Scenario 1:
You choose the car (with a 33% chance) and you win.
Scenario 2 and 3:
You choose either of the goats (and because there are two choices, there is a 66% chance of doing this) and therefore you loose.
So, it is the act of switching that produces the 33% and 66%.
To all those who continue to refuse to open their minds beyond the 50/50 result:
http://en.wikipedia.org/wiki/Monty_Hall_problem
Please read. It is basic maths.
Yeah you guys have got it right. The thing some people don’t seem to understand is that probability is the chance of something happening at the MOMENT of the choice. So you make your choice when the probabilities are 33/66. That doesn’t just suddenly change to 50/50 when you learn more information about your previous choice. Everybody knows that. It’d be sort of like if you picked one of the doors, then the host revealed BOTH the other two doors which contain goats. Does that mean that at the moment you made your choice, you had 100% chance of picking the car? Of course not!
The problem is just worded in a way which confuses the human mind. It’s all cultural. Get into pure mathematical logic mode and the answer is obvious.
Drew, you’re wrong. Answer this.
If you picked door # 1, and the game show host reveals goats in doors #2 and #3. What are the odds AT THE MOMENT that the car is behind door #1? It’s 100%. Surely you can see this.
Same logic applies to having door #3 and 1 goat revealed. AT THAT MOMENT, you have new information, and YES, THE PROBABILITIES CHANGE. You’ve affected the probabilities by revealing the goat. Capiche?
When new information is revealed, the probabilities change. Similar to the Heisenberg principle.
Hi Mark,
This is a totally different scenario that you’re talking about. You basically just said, when you toss a pair of dice and you look at the result and it’s a 7, the probability of rolling a 7 is 100%. Wow – what a brilliant revelation. Totally irrelevant to this situation however. Not all information is known to the contestant.
I think the Three Prisoners Problem summed this up best:
There are three prisoners scheduled to be executed, A, B, and C, although one will be pardoned. A asks the warden to tell him the name of one of the others who will be executed. As the question is not directly about A’s fate, the warden obliges—secretly flipping a coin to decide which name to give A if A is the one being pardoned. Assuming the warden’s truthfulness, there are now only two possibilities for who will be pardoned: A, and whichever of B or C the warden did not name. Did A gain any information as to his own fate, that is, does he change his estimate of the chances he will be pardoned? To make the analogy to the Monty Hall problem more explicit: if the warden says “B will be executed” and A could switch fates with C, should he?
Give it up Drew, I can’t believe this arguement is still going on. Take the blinkers off. There are countless flash and java demonstrations online that empirically prove the principle – just hit google. Just like in school when they get you to flip a coin 100 times to see if the probability of getting heads is 50/50 or not.. try it out for yourself.
If that doesn’t float your boat – watch this: http://www.youtube.com/watch?v=mhlc7peGlGg&NR=1
If you still don’t get it, don’t bother, you’re just not cut out for maths.
That’s a pretty good explanation in that video Tom. So do you understand what I was saying now??
Omg I’m a complete idiot sorry. Skimmed over your post and thought that you were a different poster sill making the “50/50” arguement.
why do they say “always account for variable change” in the movie. is this a semantic thing? does it mean “always account for variables changing?” or does it have a more specific technical meaning.
don’t forget this simple fact: the host has to open a door and knows where the car is … he will therefore open a goat door
I note and understand all that everyone says with regards to the proof of 2 thirds 1 third however the simple facts to me seem to be this.
You have 3 doors A, B and C
The rules are that there is 1 car behind a door and a goat behind each of the remaining 2 doors.
There then follows 3 phases of “the game”.
Phase 1…your initial choice;
Phase 2…elimination;
Phase 3…secondary choice.
At the start of the game with 3 doors to pick from you have a 1 in three chance of picking the car first time round. You may unknowingly pick the correct door however you are not given the option of opening that door. To your knowledge the odds of winning however are not favourable.
Regardless of whether the host knows the true position of the car he will eliminate 1 of the remaining 2 doors by revealing what is behind it.
As you have unknowingly picked the car he will obviously pick a goat.
Phase 3 of the game involves the host asking you whether you would like to switch and pick the remaining door. Do not forget that the host cannot force you to change your initial choice.
Having eliminated 1 of the doors you are now only left with 2 doors. Surely the 3rd phase represents a new game or challenge and therefore your success or failure will still depend upon the probability of picking the correct door from the number which are available. 1 prize from 3 represents a 33% probability of success in phase 1 as there were 3 doors. Surely then 1 prize from 2 doors represents a 50% probability of success in phase 3.
You are on true construction dealing with spin of the rules and the 2 thirds 1 third proof will only hold if one believes that the host works as an actor complicit in the deception of attempting to make you pick the wrong door. To me at least this is not mathematical.
From a psychological angle I see why one would wish to use the remaining 33% from the eliminated door. Given that in phase 3 you only have a 50/50 chance of picking the correct door you would want to use something to boost your odds. That said we know however that the eliminated door held a goat and that we are only left with an “either or decision” in phase 3. There is no third option. You are either correct to switch or correct to stick.
“Success” is dependent upon the number of choices you have proportional to the number of possibilities that present themselves…but only if truth is constant…surely? In phase 3 you have 1 choice to make between 2 doors…therefore 1 in 2 or 50/50. This holds true regardless of whether the host knows which one of the two remaining doors holds the car or not as the host has no bargaining chip. The eliminated 33% is only of use if precedent creates expectation and the host is more likely than not to be trying to pull the wool over your eyes. On balance therefore it is better to ere on the side of caution and switch. If the host has a propensity for trying to force the wrong decision then try to play the odds; Attach 33% success to one door and 67% to another…that’s fine but remember…there are still only two doors and you still only have 1 choice.
If the host knows from the start where the car is and you do not pick it in phase 1, being complicit the host will eliminate a goat and this still leaves you with a 1 in 2 chance of picking the correct door. In phase 3 (which is the important part) the bet is really…what is the probability that I picked correctly first time round? It was 1 in 3 in phase 1.. Is it still 1 in 3? No as you don’t have an “in 3” chance due to the elimination. You have an “in 2” chance. You therefore still have a 50/50 chance of “having picked correctly the first time round” as you still only have the option to stick or switch. If the tests do suggest that to switch at phase 3 will increase your odds 33% there must be another “actor” affecting the change. To say that that “actor” is the elimination of an incorrect choice seems somewhat of a cop-out.
Question. Are the proponents of the thirds therefore stating that you will always have a 2/3-1/3 split for success involving a choice of 1 between 2 possibilities? If so does this not then show a flaw or are we merely dealing with semantics.
Dude, you’re a moron. Imagine 1000 doors. Pick one. Was it the right one? Probably not. Do you really think that with DOING NOTHING WHATSOEVER, your chances suddenly and magically go up to 50% just because some stupid host opens 998 of the other doors??? SMARTEN UP!
I read it and I feel that’s many people misunderstanding this “theory”
I can say that, this “theory” have assumption.
1) the host knows which card is Car
2) the host always eliminate the card which is goat
many people argues it, but they dont’ know the behind assumption.
so they only said it is no logic, and use how many cards to explain how it wrong.
The proces is a MARKOV proces.
check out Markov Theory and conditional probability.
So if there were 4 doors, just because the host went through the trouble of opening an extra door of goat, now your probability to win with a switch has jumped to 75%? If there 10 doors, and you picked one, then the host opens 8 other doors that are goats , so your probability to win with a switch is 90% all of a sudden?
For the final 2 doors, there are 2 scenarios, if you initially picked the right one, the switch makes you lose. If you had picked a goat, the switch makes you win. If you believe anything other than the fact that it remains 50% for winning or losing, you are being ridiculous.
If the box you had chosen at the start had the car, the host removes a bunch of goats leaving you with a goat box and your original pick(with the car). You will lose with the switch.
If you had got it wrong at the start, the host carefully picks the ones with the goat and leaves out the one with the car(and of course the box you orginally picked). Now the switch makes you win.
Only 2 scenarios out of which you will get to choose 1!
Clearly nobody watched the movie properly because ben definitely states it’s called variable change because the host knew which door the car was behind and thats why he knew to switch. That was the whole point of him explaining his answer. Everything about the theory was clearly stated so there are no “if the host knew or not” to consider.
This theory is not correct!!!.1. The first round is not relevant since you still dont know where the car is. The odds of winning the car are 50% at the start of the game and still 50% after the first round.
2. If you pick the car the host has 2 other doors to choose from to show you . He has to pick one. If you dont pick the car on your first pick, he only has 1 door to show you.
3. If you pick the car on your first round and do not switch under any circumstances the hosts chances(or say another person) goes to 0% instead of 66.6%
4. 33.33% + 66.66%= 100% but then you must divide by 2 because you get 2 chances.
5. If the host could (or another person ) picked 2 doors first and he opened those 2 doors then yes it would be 66%. You have first pick and if you pick it and dont switch then the host (or other persons) chances goes to 0%. The game is 50/50 the whole tome if you play 2 rounds.
It’s fascinating to see the creative, yet completely wrong interpretations that people come up with to this (yes correct) theory. I wonder what the world looks like in the eyes of these people who have totally distorted views of mathematics??
I like the diagram presented above – I have to say. It’s quite illustrative. But, doesn’t quite illustrate everything.
Take three doors – #1, #2 and #3.
Each has a probability of holding the car of 33.33%.
So we get something like this:
66.66%
————————–
33.33% 33.33% 33.33%
Door #1 Door #2 Door #3
Taking Door #3 out, obviously leaves 66.66% in the ‘Door #2’ category.
However, full variable change must also impact the probabilities on Door #1 – afterall, we could easily also say
33.33% 33.33% 33.33%
Door #2 Door#1 Door #3
Which, by taking Door # 3 out, shows why 66.66% falls to Door #1 rather than Door # 3.
What am I really saying?
Well, between ANY two doors, there is a 66.66% chance of finding a car – the above diagram suggests that it is always behind Door 2 because of the way in which it presents the graphic. This is not accurate!!!
The key point about the Monty Hall problem is that it is optimal to change – not the fact that the car is always behind door #2!
You need to think about it in this way
Say there are 100 boxes, you chose box number 1 (i.e. 1/100 times you will be right 99/100 times you will be wrong)
The game show host then opens 98 incorrect boxes leaving you with a choice of box number 1 or the other remaining box
Is it in your best interest to swap????? OF COURSE IT IS
Yeah I think we get it now. The movie was technically correct, but explained it badly .. because … get this – IT WAS A MOVIE – not a math class 😛
What is funny is that mostly everyone’s explaination changed the entire scenario of what was really said in the movie, which by the way is correct. All the information you need to know is given.
For you 50/50 people if the scenario were different such as if you picked Door #1 & the game show host opened the door you picked & you were wrong & offered you to pick from the remaining 2 doors, the odds would be 50/50.
Only just saw the film 21 the other day and so am obviously late with my 2 pence worth. Here it goes.
My assumption – whatever option you select out of the 3 doors, bearing in mind it is a game show, the host will reveal a door with a goat behind it. therefore goat or car from your choice still leaves the host with the option of revealing at least 1 goat.
Regardless of what your choice is, if the host reveals a goat after your first selection (my whole theory rests on this assumption), then right from the beginning you only ever had 2 choices. It really doesnt matter how many options are presented, if the host is always intending on revealing a goat, then you only had 2 options, goat or car. therefore 50/50.
If my assumption about the host is correct then having 3 options is only an illusion because the one certainty is that the host will reveal a goat and give you another chance at picking the car, therefore the original choice is a waste of analytical time and only serves the purpose of letting the contestant believe there is the possibility of an increase in winning chance. It was 50/50 from the start because the initial choice is redundant.
proof.
pick door 1 (car)
host reveals door 3 (goat), 50/50
pick door 1 (goat)
host reveals door 3 (goat), 50/50
The first choice is redundant, the host will reveal a goat and give you your only meaningful selection
Hey esco1, you’re only half right. There are indeed only two choices. To switch or not to switch, but that doesn’t mean the probability of the outcome of each of those choices is identical. There is 33% and 66% chance of choosing the car respectively for those two possible choices.
Your argument is based on specious reasoning. Using your principles of logic one could say that if you are presented with the choice to eat a raw apple or eat some raw pork, there’s 50/50 chance of getting trichinosis with either choice. Wrong… there’s almost zero percent chance of getting trichinosis from eating the raw apple, and there’s a high percentage chance of getting it from eating raw pork.
Just like with the doors. 33% chance of car behind one, 66% chance of car behind the other.
esco1
Adding to what Daroo said. Try thinking about the problem again as if you didn’t know from the beginning that the game show host was going to open a door for you to see a goat.
That being said since you are presented with 3 doors to chose from at first your PROBABILITY of winning is 33%
After he opens a door (that you didn’t pick) with a goat behind it & presents you the option to switch or stay with the door you orginally picked. The question is “Is it in your best interest to switch” If you stick with your original door your PROBABILITY stays at 33% If you switch your PROBABILITY is 66% because of the two doors you didn’t pick the game show host revealed one of them to you (showing a goat) That shifts the 33% the door had before opening it to the door you didn’t pick. That’s why he said YES to switch & thanks for the extra 33% because by switching you now have a 66% PROBABILITY off winning the car.
All the information presented in the order it was presented are critical in seeing why this is true.
Basic thinking says with 2 options left you are going to win or lose (50/50) right. But variable change is a method of thinking to increase the probability of a win. That’s why when you count cards you are positioning yourself to increase your bet when there is a higher amount of high cards left in the deck. The probability is in your favor. But in the movie since you are working as a team you know to sit at a particular table when the deck is hot (or high in high cards) This increases player advantage & that’s why it’s argued that counting cards is not cheating. Cheating is knowing the next card is a high card vs. by counting cards there’s a higher probability the next card is a high card.
I think it is absolutely hilarious that some people can’t understand that it’s 66% chance to switch and will swear on their life that it’s 50%. Not only was this in a movie where they would obviously research it, it is a proven mathematical theory. What a lot of people miss i guess is when the host removes a door of the 2 remaining, he is forced to pick a goat. The host taking away a goat is part of the problem. There is a 33% chance you picked the car meaning now when theres 2 doors left it’s a 66% chance that you origonally chose a goat, so switch you crazy fool :).
Ok, I just saw the movie last night. The movie is wrong regarding the Monte Hall game. There are initially three potential configurations for the two goats (G) and the car (C).
G G C
G C G
C G G
We can assume in the Monty Hall game, he is never going to open the door with the car on the first pass. This would shorten the game and be less exciting. Given the example in the movie, we know there is a goat behind door #3. This leaves us two valid scenarios:
G C G
C G G
or:
G C
C G
Looks 50/50 to me.
Note that if you believe the argument in the movie (switching his choice improved his odds from 33% to 67%), had the kid initially selected door #2, he would have had to switch to door #1 to get the 67% advantage. With this argument, we’re back to the 50/50 argument of initially picking door #1 or door #2, because the logic in the movie says you always switch.
Remember, had the kid initially picked door #3 in the Monty Hall game, door #3 would not have been the first door revealed. Door #1 or #2 would have been revealed. This is a 50/50 game.
I’ve changed my mind. There is validity to the variable change idea as played by Monte Hall. You really are playing one guess vs. all the other possible options, that is door #1 vs doors #2 and #3. If we were to make the example more extreme, say 10 doors, and you had to hold your first guess until the end, There is only a 10% chance you guessed correctly. There is a 90% chance the car is behind one of the other 9 doors. Monte Hall will open doors from the larger group always showing you a goat until there is only your door, and one door left from the remaining group. Because Monte Hall knows where the car is and chooses not to show it to you, there is always a 90% chance the car is behind the set of doors you did not select whether there is 1, 2, or 9 doors remaining in that set. When given the chance to switch, you should switch because the larger set has been trimmed in a biased fashion. When you get down to the last two doors, you no longer have an unbiased data set. If there was a real an unbiased chance Monte Hall would expose the car before the final two doors, it would be a 50/50 game. The reason it is not a 50/50 game is because Monte Hall introduced bias into the final two options. Given 3 doors, if you stay with your original choice, you only have a 33% chance of winning.
http://www.youtube.com/watch?v=mhlc7peGlGg
For those of you who still think the Probabiltiy is 50% copy & paste this link & watch an explanation of the Monte Hall problem.
statistics- if your head is the oven and your feet are in a freezer, on average you are O.K
Ok. When I first saw this movie, I assumed like many people, that eliminating door 3 as an option left Ben with a 50% chance of choosing a car by switching his choice to door #2.
However, assuming that the gameshow host would have shown Ben a goat behind one of the two remaining doors regardless of which door Ben chose, it’s easy to see how he had a 66.6% chance of winning a car by switching.
There are three possible combinations of goats and cars behind the doors:
GGC
CGG
GCG
By learning that there is a goat behind door #3, the contestant could eliminate one possible combination (GGC). How helpful that could be I’m not sure of yet =).
Anyway, let’s say that for the contestant’s benefit, the combination used in this scenario was Goat / Car / Goat
The contestant chose Door #1. The host opened Door #3. Switch = Car
Had Door #2 been chosen, The host would have opened Door #1 or #3. Switch = Goat
Had Door #3 been chosen, the host would have opened Door #1. Switch = Car
Switching gives you a car 2/3 times, regardless of the combination of car and goats. If you switch doors after seeing a goat, the only way you can lose is if you chose the car initially. There is only a 33.3% chance of doing that.
the problem i see with this theory is that,
you have door 1 with supposely 33 pc
and door 2 with 66 ok, so what if the
host reveales door 2 and 3 and they are not the car,
well under the rules of this theory door one still only has 33
pc, but its obviously 100pc. does this make sense
or M I ON THE WRONG TRACK.
No it was still a 33% chance of you picking the car on the 1st try, that doesnt change.
The best way to make people see this is to get 3 cards from a deck of cards and pretend one of the cards is a car and the other 2 are goats. Turn them over. you will find that on your 1st pick each time you will get the car only 33% of the time. If you get to pick the other 2 cards there is a 66% chance of getting the car. Try it and you will understand better.
im sorry to say but your theory is completely wrong…
it goes like this:
we have to keep in mind that the game show host knows what is behind each door and you know nothing.
the game goes as follows:
in a game show, the host offers you a choice of door 1, 2, or 3. after you have made your choice, the game show host has to open one of the two remaining doors that does not have the car behind it…
so, with that background there are 3 scenarios
scenario 1:
1 2 3
C G G
say you choose door 1. right now you have a 33.3% chance of being correct.
the game show host then opens either door 2 or 3 to reveal a goat. let’s say he opens door 2, he then asks if you would like to change your answer and you say yes, so you change to door 3. so you lose the game
so scenario 1 counts 33.3%
scenario 2:
1 2 3
C G G
say you choose door 2. right now you have a 33.3% chance of being correct.
the game show host then opens door 3, as it is the only remaining door with a goat. he then asks if you would like to change your answer and you say yes, so you change to door 1. so you win the game
so scenario 2 counts 33.3%
scenario 3:
1 2 3
C G G
say you choose door 3. right now you have a 33.3% chance of being correct.
the game show host then opens door 2, as it is the only remaining door with a goat. he then asks if you would like to change your answer and you say yes, so you change to door 1. so you win the game
so scenario 3 counts 33.3%
so 2 out of 3 times (66.7%), if you change your answer, you will be correct and win…
hope that helps…
btw, im 16
This is very simple, if you choose a goat the host reveals the other goat and gives you another chance. That means that what you chose is a goat so it is better to switch. No need to use simple math in this damn problem because it just destroys your logical thinking!
there are NOT 3 possible combinations of goats and cars – there are 6.
1) C G1 G2
2) C G2 G1
3) G1 C G2
4) G2 C G1
5) G1 G2 C
6) G2 G1 C
if you pick door 1 with a car (cases 1 & 2), then switch after the host opens another door with a goat, you lose. if you pick door 1 with a goat (cases 3 thru 6), then switch after the host opens another door with a goat, you win. you win 4 out of 6 times = 66.666%.
This is the way I can understand 21’s explanation of the Monty Hall Game: There are 3 doors-one contains a car, the other 2 goats; X chooses door Number 1 (thus he has a 33.3% of being right). But there are 2 doors left. If he had been given 2 choices and had chosen doors 2&3 he would have had a 66.7% chance of being right.
But, as I said, X chooses door 1, and since there are 3 doors he has a 1/3 chance of being right- and a 66.7% chance of being right if he had been allowed to choose 2 doors: Doors 2&3 (since 1 had already been chosen).
Now the game show host says that door 3 has the goat. As I see it: Door 1 is still 33.3 chance of having the door. But doors 2&3 together have a 66.7% of having the car. Since the game show host says that door 3 has the goat (thus, it being eliminated as being in contention), the 66.7% chance goes to Door 2.
Thus, in effect, X has 2 choices, since 3 is eliminated. So, I suppose, if he picks Door 2, in statstical analysis he will have 66.7% chance of being right. (33.3% if chose Door 1; 66.7% if chose Door 2 and Door 3).
This theory is completely wrong. Soooooo wrong. Lets look at it this way. Lets say that each door has a certain amount of points. We’ll say that each door has 30 points making 90 points all together. If one door is eliminated, then there are no longer 90 points all together. There are now 60 points. So there are now only 30 points running against you. Lets say there are 3 guys. Two of those guys are going to jump one of those guys. Ok well lets say that each guy has equal strength. Let give them each points for their strength. We will give them 30 points each. Well if two of the guys are going to jump the other guy then that means there is 60 points of strength up against 30 points. Well if one of the two guys that is going to jump the one guy decides he doesn’t want to fight, there will then be 30 points of strength against 30 points of strength. The guy that decides not to fight can’t just give his points to his buddy. At first there wasn’t a good chance the one guy would win the fight and there was a good chance that the two guys would. Well when the one of the two guys decides not to fight, the guy who is fighting on his own now has a better chance that he can win and the guy that had a partner in the fight now doesn’t have as good of a chance as he had. He now has just as good of a chance as the other guy has. It is the same way with the doors. If one door is eliminated then it is just that; eliminated. It is no longer a factor in the problem. Without door number three there is a better chance that what you chose to begin with was correct. At first when you choose door 1, there was a 66.6% chance that what you chose was wrong and there was a 33.3% chance that what you chose was right. When door number three gets taken out of the equation, there is now a lower chance that what you chose was wrong because you now know that one of the doors that you didn’t choose was the right door to not choose. Therefor, the chance that you in fact did choose the correct door goes up as the chance that you didn’t goes down. One of the comments above this one put 10 doors into the equation instead of just 3. If there are ten doors and you choose the first door, then there is a 90% chance that what you chose is wrong. When one of the doors is opened showing that there is a goat behind it, the odds against you are less and the the odds for you are more.
Here is another way to put it. Lets say you have ten doors to choose from and you choose door number 1. 9 of the doors have a goat behind them, one door has a car behind it. If doors 3 – 9 are opened and shown to have a goat behind all of them, are you going to sit there and tell me I still only have a 10% chance I chose the right door? Of coarse you aren’t. That would just be silly. Every time a door is opened and shown to not have a car behind it, your chances get better and better that you did in fact choose the right door. An elimination of a door is an elimination of a chance against you. The less the odds are against you, the more the odds are for you. In the original example with 3 doors, you start by having a 1/3 chance because you chose 1 of “3” doors. Once one of the doors is eliminated, only 2 doors remain, so how can you say that you still have a 1/3 chance? You can’t say that because there are only 2 doors. It’s as if the third door had never existed in the first place. You can’t say that door number two has a 2/3 chance, because door number 2 is only one door, not two doors. Just because door number 2 and 3 together had the equivilant of 2/3 doesn’t mean that once door number 3 is gone then door number 2 will now be 2/3. It won’t be 2/3, but 1/2 because only 2 doors exist now. So how can you say that once door number 3 is gone that door number 2 has a 2/3 chance of being the door with the car behind it when it is only one door? You can’t say that because 2/3 only existed because it was 2 doors out of 3 doors. Now that there is only 2 doors, it cannot possibly be 2/3, it can only be 1/2. 1/2 = 50%, not 33.3%. If any of you watch deal or no deal then you know that the more brief cases that get opened that don’t have a million dollars in it, the more the banker offers the contestant depending on what values of money are left. If this theory were true then the banker shouldn’t offer the contestant more money ever. The banker would say that no matter how many brief cases are eliminated, the contestant still has the same chance they had to begin with. It wouldn’t be a very fun show then would it. As brief cases are eliminated, the contestants chances get better. In the original example, if two doors are eliminated, showing both of them to have a goat behind it, we would know that door number 1 has a 100% chance that it has a car behind it obviously. It wouldn’t have the same chance as it had to begin with.
If there were 100 doors and you picked door number 1 and doors 3-100 were eliminated leaving only door number 2 and the door you picked(#1), are you going to sit there and tell me that I still only have a 1% chance that I picked the right door and there is a 99% chance that door number 2 has the car? Of coarse you aren’t going to tell me that. That would be idiotic.
And just one more way to put it is this. If you were aloud to pick two of the three doors and you chose door 2 and door 3, you would have a 66.6% chance that you have a car. If the host opened door 1 revealing a goat behind it, you would then know that it is 100% that you have a car. You wouldn’t still have a 66.6% chance that you had it. If he then made you choose between those 2 doors, you would have a 50% chance because there were only two doors. Once there are only 2 doors, you have to divide 100 by 2, not 3, to come up with the percentage of each. This theory is the stupidest thing I have ever heard in my life. And if someone made it a law then I would seriously question all of math and science.
Hi Jonathan,
Let me point out the flaw in your logic if I can.
You said that each time a door is eliminated that it improves your chances of picking the car.
This would be true IF the doors were eliminated BEFORE you chose a door. That’s obvious, everybody knows that if you pick between two things, you have 50% chance, if you pick between 10 you have 1/10 etc.
BUT, what you are failing to account for is the fact that you picked the door FIRST – before any doors were eliminated. When you pick the door, your chances are 1/N where N is the number of possibilities. You can’t remove door #3 and alter history and go back and say you would never have picked door #3. The fact is YOU MIGHT have picked door #3 but it was eliminated. That’s a paradox.
The resolution of the paradox is actually pretty simple. The probability of picking the car is 1/N where N is the number of doors you had the option of picking AT THE TIME YOU PICKED IT. That’s set in stone. You can’t alter it.
What you CAN do, however, is use the knowledge that you’ve been granted by the opening of the other doors to realize that you are being given a gift of awareness and that switching is going to greatly improve your odds of winning.
As a final example consider the following which I hope makes it all clear:
Imagine 1000 doors, 1 car and 999 goats.
You pick Door #777
One by one the host opens each door.
Door #1 – goat. Door #2 – goat. So on and so forth.
Each time the host opens a door, does that actually change your odds?
Or are you just getting more excited that maybe you hit that 1/1000 chance?
It’s still 1/1000 chance. No matter what order the host opens the doors, it will always be 1/1000.
Just try it. Get 3 pcs. of paper. Write a c on one for car and the other 2 write g for goat. Turn them over a pick a door(paper). The odds are 66% chance thay you will pick a goat. Only 1 in 3 you will pick the car. Just keep trying this and you will soon understand that you will win more if you switch. Do it a bunch of times and write how many times you win or lose.
Actually try this. write a g (for goat) on 2 pcs of paper and write c for car on the 3rd piece. Turn the paper over and pick a paper. If you pick a g more times than a c you will know the theory is correct (which you will because there are 2 g’s to pick from and only 1 c)
This shows the theory is correct and you will win more times if you switch.
To all the non believer’s:
The reason why those who don’t agree or can’t see why this is true is because your examples & explanations are wrong to begin with. You either don’t fully understand the question/process & that there are 2 steps involved or you are adding information or scenerios that don’t pertain to the question/process
All the information that is given in the order that it is presented is all you need to know.
Watch this movie again or watch this video…(copy & paste)
http://www.youtube.com/watch?v=mhlc7peGlGg
It may help to Separate to problem/question into 2 parts/steps
The first step:
I’m sure most of you non believer’s would agree that given 3 doors to choose from your odds are 33% of picking correctly. You make your pick
Game show host opens one of the 2 doors that you didn’t pick to reveal a GOAT
The second step:
You are presented with an option to either keep your orginal choice.
or
Switch.
NOTE:
Although at this point there are only 2 remaining doors to chose from your odds are not 50/50 because if you keep your orignal choice, that choice was made when there were 3 doors to choose from (Step 1) keeping your odds of picking the correct door at 33%
As I mentioned in an earlier post that if the situation was different such as you make a choice of 1 of 3 doors & the game show host reveals the door that you picked as being a goat & presented you the option of picking between the remaining 2 doors then your odds are 50/50 but this is not the way it is in the movie or the “Monte Hall Problem”
And so Monty also asks another he also asks another contestant to pick one out of the remaining two. Whats the odds for the new player?
Here’s the real question.
Let’s say the first contestant, Bob, switched his choice (cause he saw the movie the night before). Monty is thinking “Smart man!”.
The 2nd contestant, Jane, was in sound proof room, no idea what happened beforehand.
She is brought out and Monty asks her to pick between the two remaining doors…she flips a coin to help her decide – its heads, so she picks door 1.
Monty snickers, and declares “Bob has a 66% chance of being right, Jane has a 33% chance of being right!”.
What are the chances that Monty gets nailed by the woman?
EddieC
Jane’s odds would be 50% but as far as Monty getting nailed I gues it would depend if he gives her the car or the donkey
Disagree with that logic. If you’re chances of guessing right are 66% with door #2 and door #3, then they are also 66% with door #1 and door #3, or any combination of two out of the three doors.
Gosh! I never knew that all of my college math professors were so stupid!
This is how I look at it. Lets say there are two parallel shows and the door configuration is EXACTLY the same. The contestant in show 1 chooses door 1 and the one in show 2 chooses door 2. The hosts reveal the goat in door 3, are the statistical probabilities in both rooms gonna be 66.6% for the door they didn’t initially choose? if so, both door no 1 and no 2 have a 66% chance which makes no sense at all.
Yes the statistical probabilities for both contestants are 66.6% for the door they didn’t initially choose. There is also 33.3% probabilities for both contestants for the door they did initially choose.
What wouldn’t make sense was if there were 100% probabilities for BOTH contestants for the door they did/didn’t choose.
I had to think hard about this short video to understand the concept of variable change. The premise of winning the car after switching from door 1 to door 2 doesn’t seem intuitive, or even logical, being that you only have a 50% chance after door 3 was revealed as a goat. However, when door 3 was reveled as a goat, you already won 1 selection. You didn’t get the car, but you did win a selection of, lets say, eliminating a door that had a goat. Now you are offered a second selection. Since you already eliminated 1 door with a goat, does that mean that over time you will hold a 100% record for eliminating all doors with goats? Maybe not, and since you were able to eliminate the first one already, there is a chance that the second option may not allow you to eliminate the second goat with the same choice. So you have to think that this could also be defined as a game of eliminating goats. This does not guarantee that the car will be behind door 2, but given 2 opportunities to eliminate goats, chances are you can’t eliminate them by maintaining the same choice always. So you are actually working on the premise of being 50% right and 50% wrong with the same choice. That is where the logic is, far from the emotion of believing that given a second opportunity, you will always be right with your first choice.
Yayy this makes me feel sane again. Thank you I’m not alone lol
The Monty hall problem cannot be solved with less than 100% probabilty being the outcome. Rather the problem can be solved with 100% certainty, that of an outcome being logic.
The game host would not reveal the door with the prize. In asking the contestant to change the selection, it follows that if the contestant had chosen the prize, the game host would not reveal a door with the prize. Therefore the game host “told” the contestant that the contestants choice was the prize.
So the game host “told” the contestant that the remaining door that the contestant had not chosen was not the prize, in addition to the door that the game host had revealed, was not the prize. So game host specified to the contestant those two doors that were not the prize, affirming the 100% certainty that the door that the contestant chose was the prize.
You need to be an attentive contestant that adds one plus one to get which door the prize is behind.
According to statisticians, statistics is based on probability.
In reality, statistics of probability is based on what is not suppose to exist, perpetual motion. In its most accommodating description, relative to time, is P[p(t)].
P[p(t)] is the Physics of perpetual motion as a function of time.
A person can flip a two sided coin in which each side has an unshared unique symbol with respect to its other side. Statistics states that one side will face the opposite side when the coin settles to rest, and that the side facing up has a 50 % chance of doing so. Statisticians do not quite word it this way.
In other words, statisticians set the condition that if the coin is flipped long enough, each side will face up 50% of the time.
In reality, the unique symbol on each side will always remain the same, and the conditions will always be set by the presenter.
In a clinical setting: many clinical practitioners, and/or their institutions, state they will always preform to “Evidence based practice.” I’m not sure what they really mean by this, but statistically speaking, the implied interpretation is, they practice what works.
This can be interpreted to mean, they are evaluating my condition on what has worked on similar cases. This is okay, until it’s not.
The moral of this story: Alter equations/formulas to consider the individual.
You’re assuming the host wants you to lose, haha, but it seems like a random computer simulation run a billion times would bear some results
Am I the only one who doesn’t think this makes sense or ever will?
It’s misleading.
Why is the line over the last two doors? If someone picks one door, and the host opens up one of the other doors, yeah the chances increase, but unless you can tell if the person is suggesting in their tone of voice to choose the other door, both doors still remain a risk.
Anyone can trick themselves into thinking a formula works.
It is based more on intuition and not math.
50% chance would apply to each door after one door is eliminated.
1/3 chance into a 50:50 chance.
If I am wrong, I’m sorry, but I truly cannot wrap my brain around it any other way. I was in AP calculus and my dad is an engineer. I think he would disagree with this method, but I don’t know for sure.